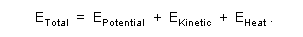
Embellishment of a conversation over email, motivated by "Mechanical Universe and Beyond" series from CalTech and PBS (CGI under development).  Most equation images generated from clipping MathCAD sessions.
From Newton's laws of motion we may derive the primary expressions for most non-relativistic mechanical interactions, so long as we keep in mind Galileo's conservation principles.

Let us consider an expression representing the total energy at any moment of a simple mechanical system to have a form resembling

(1)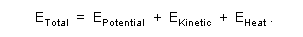
Here we construct a basic model defining the total energy of a system as the conservative sum of its potential energy (capacity to contribute work into the system), kinetic energy (current motion state within the system), and heat energy (comprising vibration, thermal, radiation, or other interaction effects). With this relationship we can express what Galileo may have had in mind concerning his experiments involving balls rolling down one inclined rail and up another to nearly the same height regardless of angle.

Observation of these experimental phenomena with reference to expression (1) might be elaborated upon as follows: The ball begins at ambient (room) temperature, with no motion (at rest), with some potential to do work related to its initial height above the floor, then once released it accelerates down the inclined rail (on account of gravity) until reaching the floor whereupon all of its hitherto available potential energy has been converted into kinetic energy related to its present motion, then proceeds across the floor some short distance and up the opposite inclined rail, converting its kinetic energy back into potential energy, until finally reaching the same height above the floor on the new rail, less some small distance corresponding to the heat energy which was dissipated into the ball, the floor, and air, due to friction throughout the experiment.

When considering elastic interactions, we assume the sum total of energy related to all current motion in a system and to all its potential for motion is conserved, so that we may omit dissipation of energy to heat from friction, specifically for the purpose of initially simplifying analytic relationships between potential and kinetic energy.

The principle of inertia basically submits the notion that the state of motion of any system is conserved unless acted upon by an application of some outside force causing change in momentum for some component of the system.

Let us now elaborate upon Newton's laws of motion in greater detail using Leibnitz's notation starting from the definition

(2)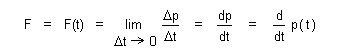
wherein force F is equivalent to the rate d/dt at which momentum p of an object or system is changing at a given instant of time t.

The notions of inertia and elastic interaction may be combined to form the notion of conservation of momentum represented in a manner such as

(3)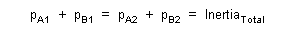
which states that the total inertia of the system of objects A and B is equal to the sum of the momenta of both objects either before or after interaction. This notion is meant to be extended as well to systems with arbitrary numbers of elements in motion, or even to changing numbers of elements from items merging or fracturing, so long as elasticity is maintained about the scope of observation.

When considering objects of unvarying mass we can demonstrate using a billiards table that expression (3) can also be written
(4)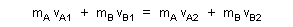
which ultimately yields
(5)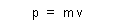
where momentum p is equivalent to the product of mass m and velocity v (matter and motion combined), for objects with speeds much less than that of light (v << c » 3 x 108 m/s).

Analyzing motion irrespective of force reveals that for a single dimension continuous position displacement function of an object defined over some time domain from t0 through t0 + Dt

(6)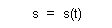
we may define velocity as instantaneous rate of change in position
(7)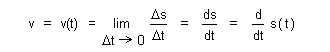
and define acceleration as instantaneous rate of change in velocity
(8)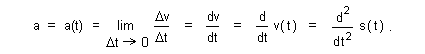
Combining expressions (2) and (5) we arrive at
(9)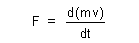
which for invariant mass may also be written
(10)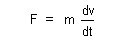
and by expression (8) becomes the familiar
(11)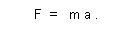
Now we begin to relate these force formulae with expression (1) by defining the various types of energy mentioned. For the present we remain focused on elastic systems, ignoring loss to heat, in order to establish a model of the relationship between potential and kinetic energy. This should shed more light on Galileo's ball and ramp observations, if we can assume that the points where the ramps meet the floor are sufficiently smooth so as to not cause the ball to bounce during the experiment, and so on.

The properties which remain consistent throughout are the mass m of the object, its acceleration due to gravity g, and the elevation y at either end.

Studies on falling bodies show that g » 9.8 m/s2 » 32 ft/s2 and essentially is constant anywhere near the surface of the earth. With this in mind we set

(12)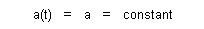
which allows us to calculate position by solving the differential equation found within expression (8). Integrating once provides our formula for velocity:
(13)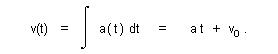
Here the constant of integration becomes initial velocity v0 which we reason from comparison with expression (7). Integrating again provides our position function:
(14)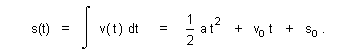
Here the constant of integration becomes initial displacement s0 . Using -g for acceleration and y for elevation we find for falling bodies
(15)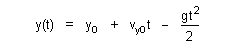
where y0 is initial height and vy0 is initial vertical speed, and friction from air resistance, etc. is omitted. This formula and horizontal speed vx(t) = constant generally describe projectile motion before factoring in resistance effects.
Careful observation of the speed at which the ball travels across the floor, once having left the first ramp, shows the same value for initial height y0 = constant and initial speed vy0 = 0 regardless of ramp slope.

We may also note that the rate of displacement, or velocity of the ball along the ramp once released from rest is found to be consistent with

(16)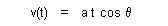
where a = g, and q is the angle between direction of gravity and the ramp, indicating significance of vector components when relating force and motion.

Analyzing this relationship for single dimension displacement we find that total change in momentum Dp is equivalent to the impulse of force through the entire time applied Dt, as shown by solving expression (2) into the form

(17)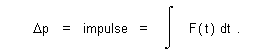
When we consider the special case of constant acceleration as by free fall or on a ramp, it follows by expression (11) that force also remains constant for the impulse duration upon an invariant mass object. With respect to the earth's surface gravity we may also define
(18)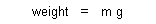
which is the force of attraction of a mass by the earth. When the object is not in motion we say by the notion of static forces that that the earth, floor, or the platform upon which the object rests is providing equal and opposite force needed for maintaining its position. When the object is in free fall we say that all resistant forces are removed causing its motion to change uniformly in accordance with expression (15) until reaching the ground or some other obstacle.

Applying constant force to an invariant mass without resistant forces we merge expressions (17), (13), (11), and (5) and obtain for impulse

(19)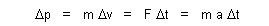
which states that change in momentum is proportional to change in velocity of a mass, and to constant force through the corresponding time duration.

This set of relationships gives us much of what we need including Dt which we could obtain by setting y to some constant height in expression (15) when considering free falling objects.

Generalizing for constant force along straight frictionless slopes we merge expressions (16) and (19) to find
(20)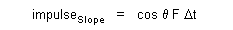
showing that the path of an object determines how its momentum is changed as it moves through a force field. And as an evenly rounded ball is allowed to roll along any sufficiently continuous path we note conformance with expression (20) exists as Dt approaches 0 about each t within the domain of unobstructed motion.

These observations serve to illustrate that acceleration of a mass along some specified path occurs at a rate corresponding to the vector component shared between the path and the force applied at any point.

Since the time required Dt for the ball to travel along a straight ramp before reaching the floor under the constant downward force of gravity is increased by the factor 1 / cos q, and since the length Ds of the ramp is also increased by the same factor 1 / cos q, the cosine terms cancel and we find the same rate of displacement ds/dt = v velocity, when the ball leaves the ramp en route across the floor for any ramp angle q, revealing the same change in momentum found by merging expressions (15), (13), and (19) with initial height y = h, constant weight Fy = -mg, and any v0.

Recognizing that elevation and gravitational force are the parameters governing a specific quantity, convertible to change in momentum, which generally relates some kind of potential work energy exchanged in accordance with force and distance, we may contribute part of expression (1) by defining

(21)
where weight and height produce potential energy which is equivalent to the work engaged for constant force applied through entire displacement in the same direction. When we change the height by some amount this relation evolves into
(22)
which may be generalized further by allowing force to vary with sufficient continuity in the direction of motion as caused by a spring or gravity so that F(s) may be found as the average value of F(s) for some s = s within any Ds within Dh as each Ds approaches 0 about each s showing work in the form
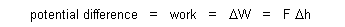(23)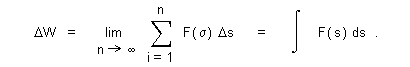
Analogy between expressions (17), (19) for impulse, and (22), (23) for work becomes more apparent, since they are meant to contribute conservatively parts to total inertia (3) of a system, and to total energy (1) of a system as force is applied over time, or displacement respectively. This relation for work though is hitherto for one dimensional displacement. Further generalization of work over any reasonably continuous path by expression (20) requires the shared vector component between force and path be accounted for in a manner such as
(24)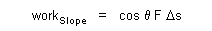
where we examine the potential difference related to constant force, perhaps weight, through some displacement along a straight frictionless slope.
As the change in height and in displacement are related by Dh = cos q Ds for each infinitesimal along any sufficiently continuous path, and as the force through this path is allowed to vary continuously also, this change in potential energy depends on the vector component shared between the force field and displacement everywhere along the path of integration, which we may express as
(25)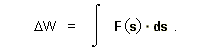
These terms herein are mostly vector valued or dependent: path function s(t) = sx(t)i + sy(t)j + sz(t)k represents a spatial variant of expression (6), showing displacement relative to 0 the vector origin; force field F(s) = Fx(s)i + Fy(s)j + Fz(s)k shows magnitude and direction consistent with and dependent upon the domain of space containing the path; infinitesimal path element ds is the differential about each s(t); and F(s)×ds = |F(s)| |ds| cos = |F(s)| |ds| cos q is the inner (dot, scalar) product of these components everywhere along this path.
This method shows work for any object following a reasonably continuous frictionless path through a force field consistent with position, and by inference a given potential energy expresses to what extent an object under position dependent force may be displaced along some such path, and correspondingly what manner of force may be engaged by means of this allowed displacement.
When we specifically examine the case where the path and force are both in the same direction throughout, as in a weight in free fall or bobbing on a spring, the inner product projection ratio cos q = 1 everywhere along the path, and as a result we find equivalence with expression (23).
Also, for constant directional force like gravity, this result is consistent with expression (21) since for every infinitesimal Fs Dsi = m g Dhi, force applied Fs = FAverage cos q is the component in common with the path differential Dsi = Dhi / cos q , hence the cosine terms cancel before integration, thus we find total potential is changed only by displacement in the direction of this constant force, as height and weight are related in this case.
Analyzing energy further so as to relate the motion it potentiates, we desire variant expression for work involving velocity v and momentum p ( = mv insofar as mass m is necessary to be knowable), and so utilize the method for change of variables under integration. Thereby considering work for single dimension displacement, we proceed with restating expression (23) in such terms as
(26)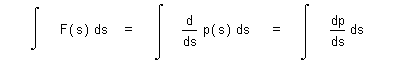
revealing momentum element dp in relation to displacement element ds, wherefrom we substitute time element dt for displacement element ds in accordance with the chain rule yielding
(27)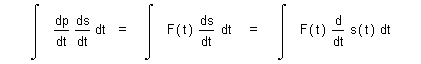
for which velocity v = ds/dt and invariant mass m may be factored in such manner as to provide the relations
(28)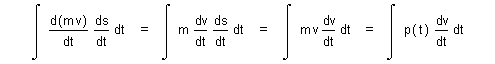
whereupon substituting velocity element dv for time element dt by the chain rule ultimately exposes
(29)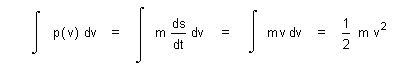
plus the constant of integration initial momentum mv0 = p0 which is ignored when initial velocity v0 = 0.
This result shows generally what total change in rate of displacement, velocity, or momentum is obtainable for an object initially at rest with knowable constant mass, as it traverses through some continuous path within a conservative related force field, given some initial value for potential work energy available, and provided that the embedded equations of motion are inherently consistent and solvable.
Recognizing this momentum formula from expression (29) is directly quantifiable in terms of energy or work we are able to contribute another part of expression (1) by defining
(30)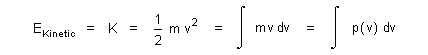
wherein kinetic energy is generally formulated from integration of the velocity dependent momentum function p(v) embedding all equations of motion over the entire change in velocity v - v0 = Dv. Moreover, with consideration given to any initial velocity v0 ¹ 0 we find the same total change in momentum from this integral by solving for Dv while mass is held constant, so long as total energy is unaffected by velocity, in other words, the path is frictionless. Also, when force is held constant without resistance, as with weight under free fall, we find that any bounds of evaluation v2 - v1 = Dv relate difference in velocity from equivalent work found for v0 = 0 and Dv = v - v0 = v where v2 - v1 = v - v0 = v as the same force is maintained everywhere.